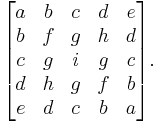Bisymmetric matrix

In mathematics, a bisymmetric matrix is a square matrix that is symmetric about both of its main diagonals. More precisely, an n × n matrix A is bisymmetric if it satisfies both A = A^T and AJ = JA where J is the n × n exchange matrix.

For example:

Properties

Bisymmetric matrices are both symmetric centrosymmetric and symmetric persymmetric. It has been shown that real-valued bisymmetric matrices are precisely those symmetric matrices whose eigenvalues are the same up to sign after pre or post multiplication by the exchange matrix^[1].

The product of two bisymmetric matrices results in a centrosymetric matrix

References